A Theory of Universal Artificial Intelligence based on Algorithmic
Complexity
Keywords: Artificial intelligence, algorithmic complexity,
sequential decision theory; induction; Solomonoff; Kolmogorov; Bayes;
reinforcement learning; universal sequence prediction; strategic
games; function minimization; supervised learning.
Abstract: Decision theory formally solves the problem of
rational agents in uncertain worlds if the true environmental prior
probability distribution is known. Solomonoff's theory of universal
induction formally solves the problem of sequence prediction for
unknown prior distribution. We combine both ideas and get a
parameterless theory of universal Artificial Intelligence. We give
strong arguments that the resulting AIXI model is the most intelligent
unbiased agent possible. We outline for a number of problem classes,
including sequence prediction, strategic games, function minimization,
reinforcement and supervised learning, how the AIXI model can formally
solve them. The major drawback of the AIXI model is that it is
uncomputable. To overcome this problem, we construct a modified
algorithm AIXItl, which is still effectively more intelligent than
any other time t and space l bounded agent. The computation time of
AIXItl is of the order t·2l.
Other discussed topics are formal
definitions of intelligence order relations, the horizon problem and
relations of the AIXI theory to other AI approaches.
Table of Contents
- Introduction
- Artificial Intelligence
- Main idea
- Contents
- History & References
- The AIµ Model in Functional Form
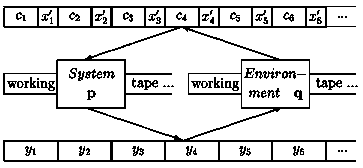
- The cybernetic or agent model
- Strings
- AI model for known deterministic environment
- AI model for known prior probability
- The AIµ Model in Recursive and Iterative Form
- Probability distributions
- Alternative Formulation of the AIµ Model
- Equivalence of Functional and Iterative AI model
- Factorizable µ
- Constants and Limits
- Sequential decision theory
- The Universal AIXI Model
- Induction and Algorithmic Information theory
- Definition of the AIXI Model
- Universality of xiAI
- Converting general functions into chronological semi-measures
- Convergence of xiAI to µAI
- Intelligence order relation
- Credit bounds and separability concepts
- The choice of the horizon
- Sequence Prediction (SP)
- Using the AIµ Model for Sequence Prediction
- Using the AIXI Model for Sequence Prediction
- Strategic Games (SG)
- Introduction
- Strictly competitive strategic games
- Using the AIµ model for game playing
- Games of variable length
- Using the AIXI model for game playing
- Function Minimization (FM)
- Applications/Examples
- The Greedy Model FMGµ
- The general FMµ/XI Model
- Is the general model inventive?
- Using the AI models for Function Mininimization
- Remark
- Supervised Learning from Examples (EX)
- Applications/Examples
- Supervised learning with the AIµ/XI model
- Other AI Classes
- Other aspects of intelligence
- Time Bounds and Effectiveness
- Introduction
- Time limited probability distributions
- The idea of the best vote algorithm
- Extended chronological programs
- Valid approximations
- Effective intelligence order relation
- The universal time bounded AIXItl system
- Main theorem
- Limitations and open questions
- Remarks
- Outlook & Discussion
- Miscellaneous
- Outlook
- The big questions
- Conclusions
BibTeX Entry
@TechReport{Hutter:00f,
author = "M. Hutter",
title = "A Theory of Universal Artificial Intelligence based on Algorithmic Complexity",
month = apr,
year = "2000",
pages = "1--62",
keywords = "Artificial intelligence, algorithmic complexity,
sequential decision theory; induction; Solomonoff; Kolmogorov;
Bayes; reinforcement learning; universal sequence prediction;
strategic games; function minimization; supervised learning.",
url = "http://xxx.lanl.gov/abs/cs.AI/0004001",
url2 = "http://www.hutter1.net/ai/pkcunai.htm",
abstract = "Decision theory formally solves the problem of rational agents in
uncertain worlds if the true environmental prior probability
distribution is known. Solomonoff's theory of universal induction
formally solves the problem of sequence prediction for unknown
prior distribution. We combine both ideas and get a parameterless
theory of universal Artificial Intelligence. We give strong
arguments that the resulting AIXI model is the most intelligent
unbiased agent possible. We outline for a number of problem
classes, including sequence prediction, strategic games, function
minimization, reinforcement and supervised learning, how the
AIXI model can formally solve them. The major drawback of the
AIXI model is that it is uncomputable. To overcome this
problem, we construct a modified algorithm AIXI-tl, which is
still effectively more intelligent than any other time t and
space l bounded agent. The computation time of AIXI-tl
is of the order tx2^l. Other discussed topics are formal
definitions of intelligence order relations, the horizon problem
and relations of the AIXI theory to other AI approaches.",
note = "62 pages, http://xxx.lanl.gov/abs/cs.AI/0004001",
